Wireless Handover Simulations
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
| Project: Wireless Handover Simulations |
|---|
| Simulations of handover in wireless communications |
| Web: | |
|---|---|
| Project leader | Susana Rodriguez de Novoa |
| Project Participants | |
| Start Date | 2012/10/15 |
| End Date | 2014/12/20 |
| Supported by | UNIK |
| Objective | Get a programming tool for simulating the handover times between wireless and mobile networks.
Establish scenarios for wireless to mobile, mobile to mobile and wireless to wireless; simulate the scenarios and discuss the results |
| Research Domain | 5G Networks |
| Keywords | Handover, Simulation, GSM, UMTS, Wifi, 802.11 |
- Factpage of Project Wireless Handover Simulations
- Wireless Handover Simulations
- Handover Scenarios
- System parameters
- Propagation models
- Antennas
- Fading
- Simulation results
- Software & Background
One of the ongoing discussions in radio systems is the required time for handover between access points. This wiki page explains the background for the software package: Radio network planning and handover: Programming framework for radio propagation and handover evaluation. It provides an overview over the phenomena, gives a set of typical input parameters for wireless/mobile simulations and presents typical results for mobile and wireless handover.
The main goal by creating the software simulation tools addressed
- Understand the typical cell/coverage sizes in mobile and wireless systems.
- Understand on how cell size and cell dimensions affect handover.
Simulations
Participants
The initial work was performed as part of the UNIK4700 course on Radio and Mobility in autumn 2012. UNIK4700H12Participants contributed to the first solution, and invite everyone to contribute to the simulation tool.
by Hege & Christine
In cellular telecommunications, the term handover or handoff refers to the process of transferring an ongoing call or data session from one channel connected to the core network to another.
The contents of this section are the main parameters & schema about the 3 scenarios that we will simulate.
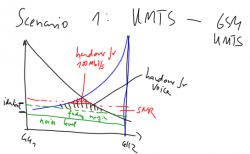
Scenario 1: UMTS, GSM handover
When a mobile user travels from one area of coverage or cell to another cell within a call’s duration the call should be transferred to the new cell’s base station. Otherwise, the call will be dropped because the link with the current base station becomes too weak as the mobile recedes. Indeed, this ability for transference is a design matter in mobile cellular system design and is call handoff.
This scenario was selected to simulate the typical handover in mobile networks.
In this scenario we assumes that a person is driving a car an talking on his cellphone. His speed is 60km/h and his driving through an urban area. When a mobile user travels from one area of coverage or cell to another cell within a call’s duration the call should be transferred to the new cell’s base station. Otherwise, the call will be dropped because the link with the current base station becomes too weak as the mobile recedes. Indeed, this ability for transference is a design matter in mobile cellular system design and is call handoff.
This scenario was selected to simulate the typical handover in mobile networks.
Input Parameters
Here are the parameters used, assuming it's in an urban area (really urban? as we discussed, urban is based on Tokyo. Thus I'd rather suggest to use suburban environment).
Frequencies:
- GSM: 1800 MHz
- UMTS: 2100 MHz
- Range between towers: 15 km - very optimistic, typical distances are between 1.5 and 3 km, see http://www.finnsenderen.no/finnsender
- Height of transmitters: 150 m - 150 m were old design, now antenna heights are typical 15 ... 30 m
- Height of receiver: 1.5 m
- Data rate: 12.2 kbps
- Equipment Temperature: 293.15 K (20 celsius)
- Traveling at 60 km/h
Analysis and explanation
Handover between GSM and UMTS, assuming same height of the transmitter towers, and that receiver height is consistent.
- Hit fading margin for GSM at: 9.9745 km, -114.2460 dB.
- Hit fading margin for UMTS at 8.8655 km, -114.4200 dB.
- This gives us a stretch of 3.8400 km where we can perform handover successfully between GSM and UMTS.
- We have around 3 minutes and 50 seconds to complete the handover at current speed.
- Between UMTS/UMTS, we have a stretch of 2.7310 km where we can perform handover.
- We have around 2 minutes and 43 seconds to complete the handover at current speed.
To se the full code and tables, see Click here to go to Simulations...
Conclusions
With these parameters we have 3 minutes and 50 seconds to complete handover (GSM - UMTS). The handover would be successful without a break.
Between UMTS-UMTS, we have approximately 2 minutes and 43 seconds to complete a successful handover.
Scenario 2: Leaving the ferry
The handoffs between WLAN and UMTS have attracted a great deal of attention in all the research areas of the wireless network, due to the benefit of utilizing the higher bandwidth and lower cost of WLAN as well as better mobility support and larger coverage of UMTS.
This scenario was selected to simulate the typical handover between WLAN & mobile networks.
We want to achieve a soft handover between wlan (on the ferry) that the mobile node is connected to when it is under deck (no other cell coverage) and UMTS (3G) when the car is driving out of the ferry. Our assumptions is that the car drives approximately 20 km/h Depending on the estimation of the break we want to find out when we have to start the handover process. While leaving the ferry the wlan signal gets weaker and weaker, and the UMTS stronger. While moving out of wlan coverage, when do we have to start the handover procedure without a break (hard handover) so that the person in the car can continue to have a conversation (ex. Skype) even though he loses the wlan connection and gains the UMTS coverage.
To determine when to start the handover, we have to base it on how fast we lose the signal fron the wlan, and how much time we need for a handover. These can be estimates. There are different parameters in WLAN and UMTS, and these has to be taken in consideration when simulating this scenario. Wifi also has less range than UMTS.
Input Parameters
- Suburban area
- Frequencies:
- 802.11b: 2400 MHz
- UMTS: 2100 MHz
- Range between towers: 1 km
- Height of transmitters:
- 802.11b: 7 m
- UMTS: 20 m
- Height of receiver: 1.5 m
- Traveling at 20 km/h
- UMTS signal strength 1W = 0 dB
Analysis and explanation
This was a very difficult scenario to find parameters to and to simulate and we didn't get any good results from the simulation.
Conclusion
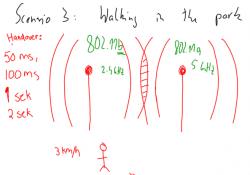
Scenario 3: Walking in the park
A handoff in 802.11 is the process that allows a wireless client (STA) to change of access point (AP). When the STA detects degradation of the communication quality, it considers changing of access point and eventually decides to perform a handoff to a candidate access point that offers better quality of signal.
This scenario was selected to simulate the typical handover between WLAN networks.
This scenario was selected to simulate the typical handover between WLAN networks. A person is walking in the park at 3 km/h. With a handoff time of 50 ms, 100 ms, 1 sec and 2 sec, how big will the potential overlap be from a 802.11b 2.4 GHz antenna to a 802.11a 5 GHz antenna?
A handoff in 802.11 is the process that allows a wireless client (STA) to change of access point (AP). When the STA detects degradation of the communication quality, it considers changing of access point and eventually decides to perform a handoff to a candidate access point that offers better quality of signal.
This scenario was selected to simulate the typical handover between WLAN networks.
Input Parameters
- Suburban area
- 802.11a: 5200 MHz
- 802.11b: 2400 MHz
- Range between towers: 50 m
- Height of transmitters: 4 m
- Height of receiver: 1.8 m
- Data rate: 12.2 kbps
- Temperature: 293.15 K
- Traveling at 3 km/h
Conclusion
We never hit the fading margin, and should have no problems doing handovers.
by Håvard
Sensitivity in a receiver is normally defined as the minimum input signal required to produce a specified signal-to-noise ratio at the output port of the receiver and is defined as the mean noise power at the input port of the receiver times the minimum required signal-to-noise ratio at the output of the receiver.
This scenario was selected to simulate the received sensitivity, the noise level, bandwidth and noise figure parameters, considering their relation in the communications systems.
Output Parameters
- ResSense =Receiver Sensitivity
Noise and noise floor
When dealing with wireless systems, we always have to calculate a noise floor. This is the "ground" noise that the received signal have to be above, for the receiver to understand the message sent. Picture yourself in a crowd at the mall (a rainy saturday), trying to speak to your friend. There exist a noise floor produced by the crowd, and your friend have to speak louder than the crowd for you to be able to hear him.
Thermal noise
The noise can come from various places, but the noise floor is consisting mainly of the thermal noise in the receiver. Whenever we are dealing with electronics, we will have to consider thermal noise. The electric energy is carried by electrons and as thees electrons is exposed for a temperature they will react by moving in random. And the higher the temperature, the more movement will the electrons have and the more thermal noise we get. This is why some radio telescopes receiving very weak signals from space, is cooled with liquid nitrogen. Thermal noise is give by this formula;
- k is the Boltzman constant
- T is temperature in Kelvin and
- B is the bandwidth in Hz
and in dB
We can also see that the bandwith is considered, as the total thermal noise is a sum of the thermal noise for each Hertz (every oscillation is affected by the randomness of the electrons).
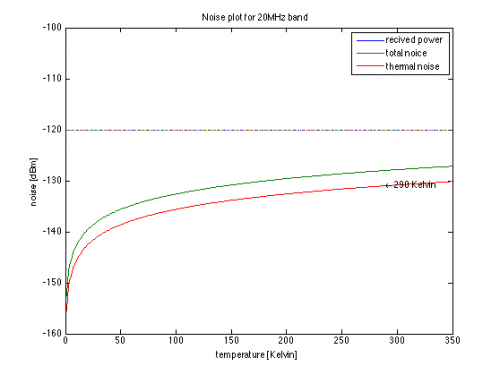
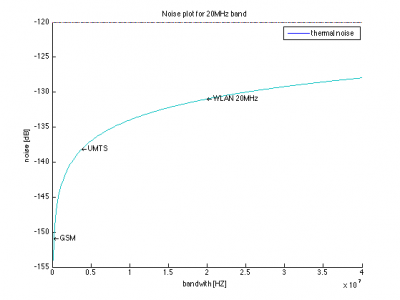
Fig 1 shows the correlation between the temperature and the thermal noise
Other noise factors
There are other noise factors we have to consider in addition to thermal noise. This is all the components playing a role from the antenna to the receiver, called installation loss. Here we have loss/noise in cables and connectors. This is typically 2-4dB We also have to consider a noise figure witch is a ratio of SNR in and SNR out of a recover. Typically 2-3dB
SNR
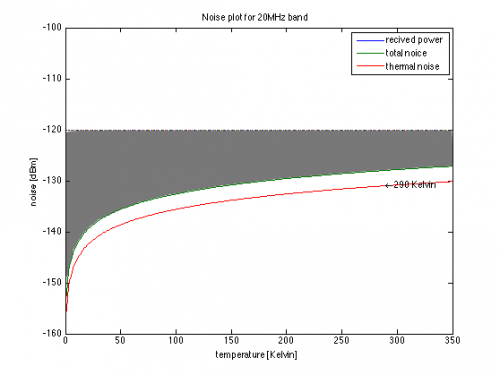
Signal-to-noise ratio is the ratio between received power and the noise given by the formula below
and in dB
The SNR is illustrated by the shaded area in fig 2
Implementation
The implementation In the implementation I programmed a small function to calculate the noise floor and the receiver sensitivity. The code is written in Matlab and is given bellow.
function [ ResSence ] = Srdb( Bw, F, temp, Lr, datarate) %SRDB Calcultates the reciver sensitivity in dB % Detailed explanation goes here % Bw = Bandwith in KHertz % temp = temprature in Kelvin % Lr = implementation loss % F = noicefigure, 3dB % datarate in kbps % fixed Eb/N0 = 5 dB EbN0=5; k=1.38*10^-23; %Boltzmann konstant ktb=10*log10(k*temp*Bw*1000)+30+F %Thermal noice in dBm prgain=EbN0-10*log10(Bw/datarate) Noice=ktb+Lr ResScence=ktb+Lr+prgain end
In our simulation we had to do some assumptions. The nose figure was fixed to 3dB. Background for this assumption is that this value is typically between 1.5dB and 4dB. The Eb/N0 was fixed to 5dB. This assumption we did on background of Widermind UMTS capacity document.
Since the thermal noise depend on the bandwidth (showed in fig 3), the thermal noise will be a bit different in the different scenarios. But the typical value (for thermal noise) is
- GSM -150dB
- UMTS -138dB
- WLAN 20MHz -130dB
These values is marked in fig 3.
In our implementation we added a "process gain" which spreads the signal (and the noise) over a wider band. This gives us about +20dB for receiver sensitivity (we logical reduce the noise with 20dB).
System parameters for WiMAX 802.16e
| Parameter | Value | Unit |
| BSS/SS Transmit Power | 43/23 | dBm |
|---|---|---|
| BSS/SS Noise figure | 4/7 | dB |
| Carrier Frequency | 2.35 | GHz |
| Bandwidth | 10 | MHz |
| Path loss model | L = 128.1 + 37.6 log 10(d) | L in dB, d in km |
| Lognormal Shadowing standard deviation | 8 | dB |
| BS antenna 3 dB beamwidth | 70 | deg |
| Cell radius | variable | km |
| Reuse scheme | 1x3x1 and 1x3x3 |
Louay and Alex have simulated the coverage of a 802.16e/WiMAX system[1]. They use the following system parameters
Their simulation show that the cell radius, based on 70% probability, 50% load and 4 antenna MRC receiver, is:
- 650 m with SNR=11 dB
- 1.5 km with SNR=1.7 dB
I assume that working with a 2 Rx antenna will reduce with a factor of 2, meaning range = 300 m with SNR=11 dB and 750 m with SNR=1.7 dB
The downlink coverage is about 1.6 km, giving a transmit power W and a probability of 70%.
References
- Thorvalden & Henne; Planning line-of-sight radio relay system
- Staillings; Wireless Communications and Networks
- http://en.wikipedia.org/wiki/Noise#Non-acoustic_noise
- http://en.wikipedia.org/wiki/Thermal_noise
- http://en.wikipedia.org/wiki/Noise_figure
by Joachim
A radio propagation model is an empirical mathematical formulation for the characterization of radio wave propagation as a function of frequency, distance and other conditions. A single model is usually developed to predict the behavior of propagation for all similar links under similar constraints. Created with the goal of formalizing the way radio waves are propagated from one place to another, such models typically predict the path loss along a link or the effective coverage area of a transmitter.
This scenario was selected to simulate the typical values for path loss in rural, urban and indoor environments.
Parameters
Input Parameters
- Dist= distance
- Freq= frequency
- C= Speed of light
- Lamda= Lamda, Wavelength
- TX_Ht= Height of transmit antenna
- RX_Ht= Height of receive antenna
Output Parameters
- FreeSpace= Free Space Model (Urban)
- Okumura = Okumura Model (Urban)
- Hata_Urban= Hata Model (Urban)
- Hata_Suburban = Hata Model (SubUrban)
- Hata_Open = Hata Model (Open Areas)
- Lee_Philadenphia = Lee's Urban Model (Philadelphia)
- Lee_Newark = Lee's Urban Model (Newark)
- Lee_Tokyo =Lee's Urban Model (Tokyo)
- Lvehicular = ETSI vehicular
Models
There are several kinds of radio propagation models. I'll explain the ones we've used in our scenarios.
Free Space
The Free Space path loss (often referred to as FSPL), is the loss in signal strength from a line-of-sight path through free space, with no obstacles nearby to cause reflection or diffraction. The model does not take the gain of the antennas into consideration, and does not take hardware imperfections into consideration.
Okumura
The Okumura model for urban areas, is a radio propagation model that was based on analysis of data collected in the city of Tokyo, Japan. It consists of three modes; urban, suburban and open areas. The urban mode was used as base for making the two other modes.
The Okumura model is very ideal for use in cities with man urban structures (as long as it's not many tall, blocking structures), and was also used as the base for the Hata model.
The model is one of the most widely used models for signal prediction in urban areas, and is applicable for frequencies in the range 150 MHz to 1920 MHz (some use it for frequencies up to 3000 MHz as well). It can be used for distancess of 1 km to 100 km, where the base station antenna heights can range from 30 m to 1000 m, and mobile station antenna height between 1 m and 10 m.
The Okumura model is expressed as:
where,
L = The median path loss. Unit: Decibel (dB)
LFSL = The Free Space Loss. Unit: Decibel (dB)
AMU = Median attenuation. Unit: Decibel (dB)
HMG = Mobile station antenna height gain factor.
HBG = Base station antenna height gain factor.
Kcorrection = Correction factor gain (such as type of environment, water surfaces, isolated obstacle etc.)
Hata model
The Hata model (also known as Okumura-Hata model, since it was based on the Okumura model), is one of the most widely used propagation model for cellular transmission prediction in urban areas. The Hata model takes the information from the Okumura model, and developed it further by taking diffraction, reflection, and scattering, into consideration. It also has two more modes; suburban and open areas.
The model is suited for both point-to-point, and broadcast transmissions.
The model is suited for frequencies in the range 150 MHz to 1500 MHz (we see that it doesn't go as high as the Okumura model, even though the Hata model is based upon the Okumura model). It can be used for distances of 1 km to 20 km, where the base station antenna heights can range from 30 m to 200 m, and mobile station antenna height between 1 m and 10 m.
Lee's model
Lee's model is applicable only to flat areas (otherwise, significant prediction errors may be introduced). The different Lee models can be summarized as follows:
ETSI vehicular
The ETSI vehicular is for larger cells (typically a few km). TX power 24 dBm for mobile phone, transmit antenna height ![]() over roof top (typical 15 m), distance r in km, f = 2000 Unik/MHz
over roof top (typical 15 m), distance r in km, f = 2000 Unik/MHz
Path loss model:
MATLAB Code
The MATLAB code used in the simulation consists of a single function, that returns calculations based on certain input parameters. One of the input parameters defines what model is to be used in the calculation.
There are 5 input parameters for the function;
- Distance (the to-distance, the from-distance is statically specified to 1)
- Frequency
- Transmit antenna height
- Receive antenna height
- Model (what model to calculate with)
The actual MATLAB-code;
function [ Dist, PathLoss ] = pathloss(distance, freq, txh, rxh, model)
% Function that returns pathloss as a result to distance
Dist=1:distance; % Distance (from:to)
Dist_Km=Dist; % Distance in km
Dist_m=Dist*1000; % Distance in meters
Dist_Log_Km=log10(Dist_Km); % Distance in Log scale (for km)
Dist_Log_Meter=log10(Dist_m); % Distance in Log scale (for meters)
Freq=freq; % Frequence
c=3*1e8; % Speed of light
lamda=c/(Freq*1e6); % Lamda/wavelength
TX_Ht=txh; % Height of transmit antenna
RX_Ht=rxh; % Height of receive antenna
% Free Space Model (Urban)
FreeSpace=10*log10((Dist_m*pi*4).^2/lamda^2);
% Okumura Model (Urban)
Lf = FreeSpace; % Free Space Propagation Loss
Amu = 35; % Median Attenuation Relative to Free Space (900 MHz and 30 Km)
Garea = 9; % Gain due to the Type of Environment (Suburban Area)
Ghte = 20*log(TX_Ht/200); % Base Station Antenna Height Gain Factor
if(RX_Ht>3)
Ghre = 20*log(RX_Ht/3);
else
Ghre = 10*log(RX_Ht/3);
end
Okumura=Lf+Amu-Ghte-Ghre-Garea;
% Hata Models
PAR_H=3.2*((log10(11.75*RX_Ht))^2)-4.97;
Hata_Urban=69.55+26.16*log10(Freq)-13.82*log10(TX_Ht)-PAR_H+((44.9-6.55*log10(TX_Ht)))*(Dist_Log_Km);
Hata_Suburban=Hata_Urban-((2*(log10(Freq/28))^2)-5.4);
Hata_Open=Hata_Urban-((4.78*(log10(Freq))^2)+(18.33*log10(Freq))-40.94);
% Lee's Urban Model for Philadenphia, Newark and Tokyo
ALPH1=(TX_Ht/30.48)^2; % alpha1: Base station antenna height
if(RX_Ht>10)
ALPH2=2
elseif(RX_Ht<3)
ALPH2=1
else
ALPH2=(RX_Ht/3)^2; % alpha2: Mobile station antenna height
end
ALPH3=10^(6/40); % alpha3: Base Station antenna gain is 6/4 dB corresponding to 10^(6/40) actual value
ALPH4=1; % alpha4: (freq/900)^-n # Assuming 900MHz
ALPH5=0.25; % alpha5: -6dB corresponding to 0.25 actual value
ALPH0=ALPH1*ALPH2*ALPH3*ALPH4*ALPH5;
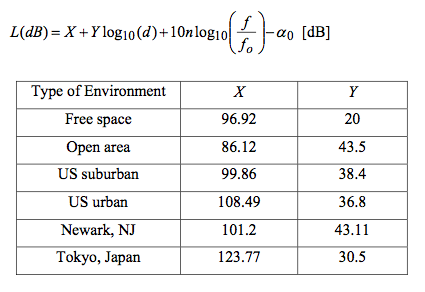
Lee_Philadenphia=108.49+36.8*(log10(Dist_Km))-10*log10(ALPH0);
Lee_Newark=101.20+43.1*(log10(Dist_Km))-10*log10(ALPH0);
Lee_Tokyo=123.77+30.5*(log10(Dist_Km))-10*log10(ALPH0);
% ETSI vehicular
% Lvehicular = 40 ( 1-4*10^-3 TXH ) log r - 18 log TXH + 21 log f + 80
ETSI=40*(1-4*(10^-3)*TX_Ht)*(Dist_Log_Km)-(18*Dist_Log_Km)+(21*log10(Freq)+80);
PathLoss=0; % empty variable
if(model==1)
PathLoss=-FreeSpace; % 1: FreeSpace
elseif(model==2)
PathLoss=-Okumura; % 2: Okumura
elseif(model==3)
PathLoss=-Hata_Urban; % 3: Hata Urban
elseif(model==4)
PathLoss=-Hata_Suburban; % 4: Hata Suburban
elseif(model==5)
PathLoss=-Hata_Open; % 5: Hata Open
elseif(model==6)
PathLoss=-Lee_Philadenphia; % 6: Hata Urban
elseif(model==7)
PathLoss=-Lee_Newark; % 7: Hata Urban
elseif(model==8)
PathLoss=-Lee_Tokyo; % 8: Hata Urban
elseif(model==9)
PathLoss=-ETSI; % 9: Hata Urban
else
PathLoss=PathLoss; % not a valid model; return 0
end
end
Discussion
Josef: Suggest that we in later courses
- analyse the effect of the propagation models. Most of them come from the early times of NMT and GSM (450 and 900 MHz), and their validity on (a) antennas on street level and (b) higher frequencies is not sure.
- look at different models, and compare the models.
by ...
An antenna is an electrical device which converts electric power into radio waves, and vice versa. It is usually used with a radio transmitter or radio receiver. In transmission, a radio transmitter supplies an oscillating radio frequency electric current to the antenna's terminals, and the antenna radiates the energy from the current as electromagnetic waves. In reception, an antenna intercepts some of the power of an electromagnetic wave in order to produce a tiny voltage at its terminals, that is applied to a receiver to be amplified.
Antennas are essential components of all equipment that uses radio and this scenario was selected to simulate the typical values for the (omnidirectional/directional) antennas.
Presentation of different communication antennas
WIFI Antennas
WIFI Antennas are used in Wireless local area networks. The maximum permitted radiated output power of a wi-fi device (In Europe) is 0.1 Watt (20 dBm). On a typical WLAN, Receiver Sensitivity will range from -20 dBm (very close to the AP) to -95 dBm (away from the AP).
Omni directional WIFI Antennas
Omni directional antennas are most commonly used to create hot spots by transmitting a signal over a large area in all directions or receiving signals in all directions when the transmit location is unknown or close by. Omni directional WiFi antennas do not need to be pointed since their radiation cone is 360 degrees, working in all directions. Each specific antenna has a gain rating or dBi (decibel isotropic) number which coincides with the performance. The higher the dBi rating the larger the area the signal covers.
Typical antenna gain values of omni directional antennas lie in the area of 6 to 9 dBi gain.
Directional WIFI Antennas
Directional antennas as the name implies refers to signal coverage in a specified direction. Unlike omnidirectional antennas, directionals must be aimed in the direction of the signal transmitter or receiver which can be for example a router or WiFi hotspot. When it comes to aiming the antenna the user must be right on the signal for the best strength and quality. The way to ensure your aim is best is to know the width of the reception cone in which the antenna has. A good way to start without seeing actual lab data or knowing the specs is to judge by the dBi (decibel isotropic) rating. The higher the dBi rating the narrower the reception cone and knowing these data points you can then begin to narrow down the right antenna for you. As a rule of thumb to remember, high dBi rating = further distance covered but not area.
Typical antenna gain values of directional antennas lie in the area of 12 to 18 dBi gain.
GSM Antennas
GSM receiver sensitivity specification is –102 dBm.
Transmitted power from BTS: Usually 43 or 46 dbm
BTS towers usually have a gain of 14-18 dBi.
Maximum power for a cell phone using GSM is 33 dBm, and usually have a gain of 2.2dBi.
To the right you can see a cell tower and a GSM phone
UMTS Antennas
UMTS Receiver sensitivity: Node B: -121 dBm, Mobile -117 dBm .
Transmitted power from BTS: 43 dbm
Node B towers usually have a gain of 14-18 dBi. Maximum power for a cell phone using UMTS is 21 dBm, and usually have a gain of 2.2 dBi.
To the right you can see a Node B Antenna and a UMTS phone
References
http://www.celtrio.com/support/documentation/coverazone/2.0.1/basics.sensitivity.html
http://www.systerra.de/documents/MOXA_WLAN_Antennas_DS.pdf
http://www.ece.ucsb.edu/yuegroup/Teaching/ECE594BB/Lectures/RF-receiver-basics.pdf
http://www.umtsworld.com/technology/wcdma.htm
http://www.autonomic-communication.org/teaching/ais/slides/1112/FoKePaHe_3G2002-TiltEffec%20ts.pdf
by Ali
In wireless communications, fading is deviation of the attenuation affecting a signal over certain propagation media. The fading may vary with time, geographical position or radio frequency, and is often modeled as a random process. This scenario was selected to simulate the typical values of fading margin, showing how it affects the system.
Parameters
Input Parameters
-
=Speed of light, 299792458 m/s
-
=speed
-
=frequency
- Probability = probability distribution of the fading
Output Parameters
- slow_fade = slow fading= fade_margin
- average_fade_duration = fast fade
Analysis and explanation
Fading is a form of attenuation that happens to a wireless signal propagating in a medium once it arrives to the receiver. The attenuation can happen over time, position and frequency. Usually, it is required to predict what type of fading will occur and try to compensate for its presence if possible. If the received signal witnesses a significant attenuation below a significant level (receiver sensitivity level) for a certain amount of time, the connection between the transmitter and the receiver will be broken. There are different types of fading but in general can be classified into two categories:
Large Scale Fading
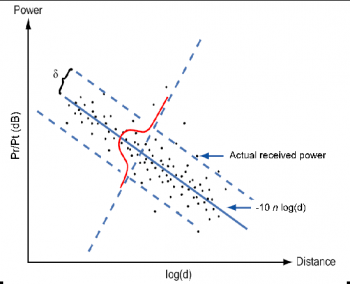
Known also as shadowing or Log-Normal shadowing. It happens when the receiver goes behind a hill or inside a building. As a consequence there is no longer a direct path from the transmitter to the receiver. The power of the received signal then will no longer be constant and it will vary following a log-normal distribution, with a mean centred at the path loss received power and a standard deviation that can be obtained statistically.
From reference (Image-1), the value of the standard deviation can be approximated as follows for frequencies between 1GHz - 6GHz.
The concept of the log normal distribution is that 50% of the time, the power of the received signal will be above or below the path-loss calculation. This leads to introducing the concept of a fade margin F, where you have the power of the received signal above the mean by ‘F’ dBs for ‘p’ percentage of time. In other words, for a given ‘percentage of time, we can search for a fading margin F, where the power received signal is above the mean.
Small Scale Fading
This can be caused by different effects. First is the multipath effect that can lead to deep feeds within small distances. Another effect is the Doppler Effect where the transmitted signal witnesses small frequency variation due to mobility.
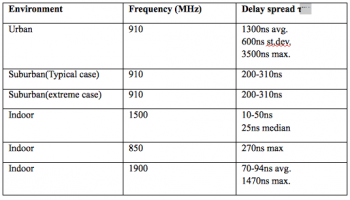
- Multipath fading: This works for both mobile and fixed wireless systems. Two or more copies of the same transmitted signal can arrive at the receiver where they have witnessed different attenuations and different phase shifts during their trip. Depending on their values, once summed together at the receiver, they can lead to a deep feed in the signal when their phases are 180 degree out of phase. The difference between arrival times of different copies o f the transmitted signal is referred to as delay spread. According to [2] , the table below presents typical measured values.
- Flat fading: This happens when the channel shows a constant gain and linear phase over a bandwidth which is greater than the transmitted signal’s bandwidth. In terms of time, this is equivalent to say delay spread is smaller than the transmitted symbol period.
- Frequency selective fading: It happens when the delay spread is greater than the transmitted symbol period. This leads to receiving a copy of the first symbol when receiving the second symbol too. This is intersymbol interference (ISI) caused by the channel.
A common rule of thumb, a channel is flat fading if Ts ≥ 10τ and is frequency selective if Ts < 10 τ.
- Doppler Effect fading: Doppler shift happens when the transmitter and/or the receiver are moving. In its simplest form, assume the transmitter is fixed and the receiver is moving at a speed v away from the transmitter. Then the apparent change in frequency, fd, is given as:
where is the wave length of the transmitted signal.
- Fast fading: It occurs when the channel changes quite fast during the period of one symbol. This happens when the bandwidth of the transmitted signal is smaller than the Doppler spread fd.
- Slow fading: It is the opposite of fast fading where the channel changes at a rate slower than the period of one symbol. This also happens when the bandwidth of the transmitted signal is much greater than the Doppler spread fd.
References
- 1. Wireless and Cellular Communication, Thomas Schwengler, Class notes for TLEN-5510-Fall 2012. Chapter 4. http://morse.colorado.edu/~tlen5510/text/classweb.html#.
- 2. Wireless Communication Principles and Practise, 2nd edition, Theodore S. Rappaport, 2002, Chapter 5.
by Thomas
Work with all the results together and apply them in the scenarios for obtaining a general overview about the main differences in the wireless communications.
Input Parameters
Propagation model (number from 1-9)
- 1: Freespace
- 2: Okumura
- 3: Hata Urban
- 4: Hata Suburban
- 5: Hata Open
- 6: Lee Philadelphia
- 7: Lee Newark
- 8: Lee Tokyo
- 9: ETSI
Other parameters used in the code for each scenario
- Needed for pathloss:
- Distance from transmitter to receiver
- Frequency in MHz
- Transmitter height
- Receiver Height
- Needed for total received signal:
- Output power
- Gain in receiver
- Gain in transmitter
- Needed for receiver sensitivity:
- Bandwith in KHz (channel)
- Temperature in Kelvin
- Implementation loss, used 3 dB
- Noisefigure, used 3 dB
- Datarate in kbps
- Needed for fading margin:
- Receiver sensitivity
- Frequency in MHz
- Probability, used 95%
Output Parameters
- Graph
- Coordinates of pathloss intersecting with fading margin [x1,y1,x2,y2] where x1 and x2 is the distance from base station where signal reaches fading margin, and y1 and y2 is the loss at that point.
Analysis and explanation
Graph data
- Receiver sensitivity is calculated by Håvard's function and displayed as a constant blue line.
- Fading margin is calculated by Ali's function and displayed as a constant red line. Receiver sensitivity is added to the result from the fading margin function before it is displayed, in order to display it in the appropriate position.
- Path loss is calculated by Joachim's function. Signal strength is calculated by adding this number to the gain from receiver and transmitter, as well as the power transmitted.
Keep in mind that models are not meant to be used for distances below 1 km, and data in those areas can be unreliable.
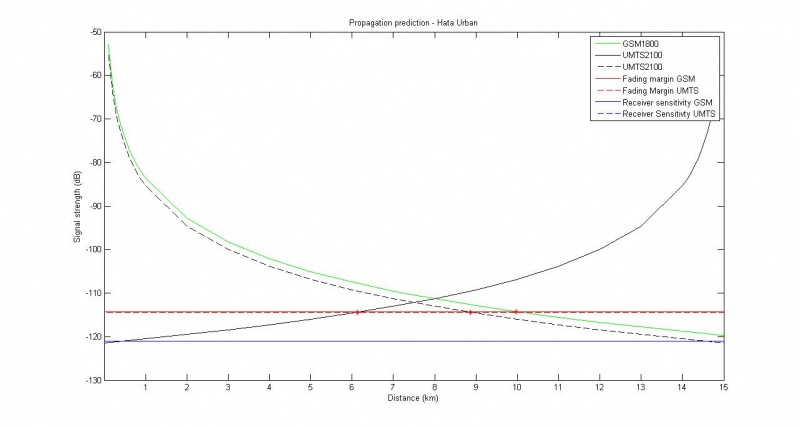
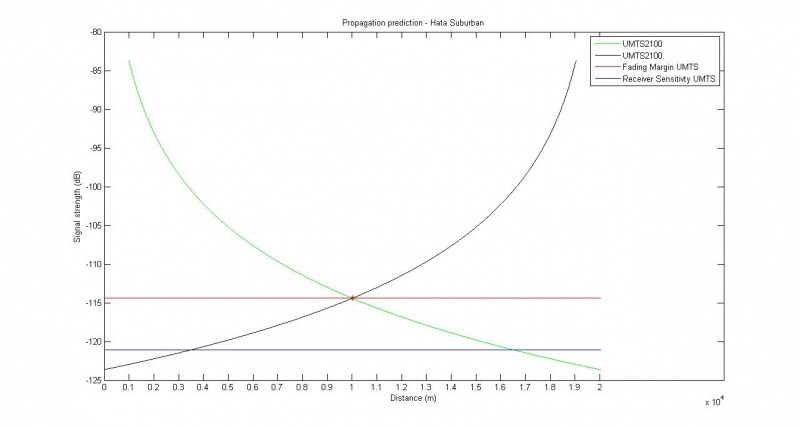
Scenario 1
Handover between GSM and UMTS, assuming same height of the transmitter towers, and that receiver height is consistent.
Used parameters
- Using parameters provided by scenario group:
- Urban area
- Frequencies:
- GSM: 1800 MHz
- UMTS: 2100 MHz
- Range between towers: 15 km
- Height of transmitters: 150 m
- Height of receiver: 1.5 m
- Data rate: 12.2 kbps
- Temperature: 293.15 K
- Traveling at 60 km/h
- Collected other data from Media:201211UNIK4700-BlockSeminar.pdf, page 9
Results
- Hit fading margin for GSM at: 10.0 km, -114 dB (or dBm?).
- Hit fading margin for UMTS at 8.9 km, -114 dB.
- This gives us a stretch of 3.8 km where we can perform handover successfully between GSM and UMTS.
- We have around 3 minutes and 50 seconds to complete the handover at current speed.
- Between UMTS/UMTS, we have a stretch of 2.7 km where we can perform handover.
- We have around 2 minutes and 43 seconds to complete the handover at current speed.
Code can be viewed at this page: Scenario_1_code
Discussion
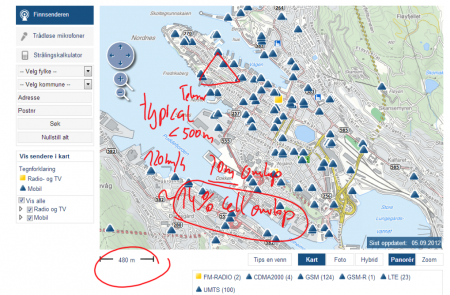
The simulation results estimated a GSM (1800) cell range of 10 km, and a UMTS (2100) cell range of 8.9 km. Such a cell size is too optimistic for urban areas, as realistic antenna constellations taken from the online repository of the Norwegian Post and Telecommunication Authority "finnsenderen" show. The typical distance between UMTS antenna towers in Bergen is lower than 500 m. Table 2 shows the estimation of required cell overlap for such a realistic network as a function of the velocity of the mobile phone. Results indicate that a 200 ms handover time will require a a cell overlap of 7.2% at a driving speed of 50 km/h, a value which is in correspondence with operational networks.
| speed (km/s) | distance/s (m) | 200 ms handover (m) | overlapp (%) |
| 3 | 10.8 | 2.2 | 0.43% |
| 5 | 18 | 3.6 | 0.72% |
| 50 | 180 | 36 | 7.2% |
| 120 | 432 | 86 | 17.3% |
Check fading margins, Cardoso and Correia suggest the following values for the fading depth: 18 dB for rural areas and 12 dB for urban areas in GSM, and 8.7 dB for rural and 5.1 dB for UMTS [2]
See also:
- The COST231-Hata model is represented in [3].
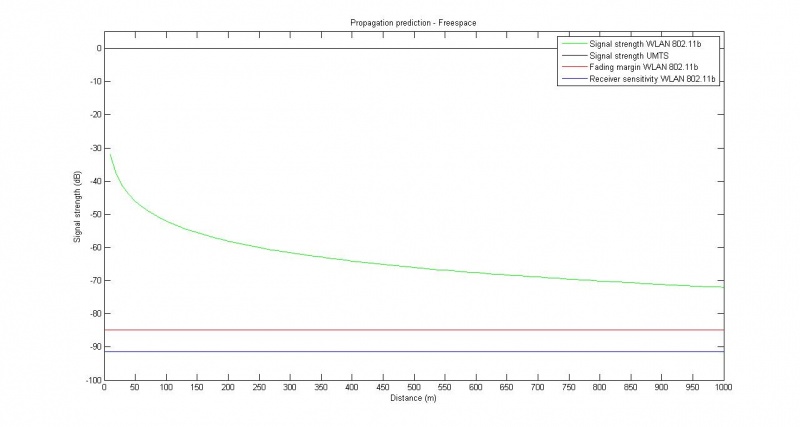
Scenario 2
Handover between 802.11b and UMTS.
Used parameters
- Using parameters provided by scenario group:
- Suburban area
- Frequencies:
- 802.11b: 2400 MHz
- UMTS: 2100 MHz
- Range between towers: 1 km
- Height of transmitters:
- 802.11b: 7 m
- UMTS: 20 m
- Height of receiver: 1.5 m
- Traveling at 20 km/h
- UMTS signal strength 1W = 0 dB
- Collected other data from Media:201211UNIK4700-BlockSeminar.pdf, page 9
- Assuming data rate of 11Mb/s for 802.11b
Results
Provided parameters suggest that UMTS signal level is a constant, due to the small area we are examining. However, the models/pathloss function do not allow distances below 1 km (with the exception of the freespace model).
These results are rather useless, as they do not take real-world reflection, diffraction, refraction, and absorption into account. Expected range for 802.11b should be around 30-150 m.
Code: Scenario_2_code
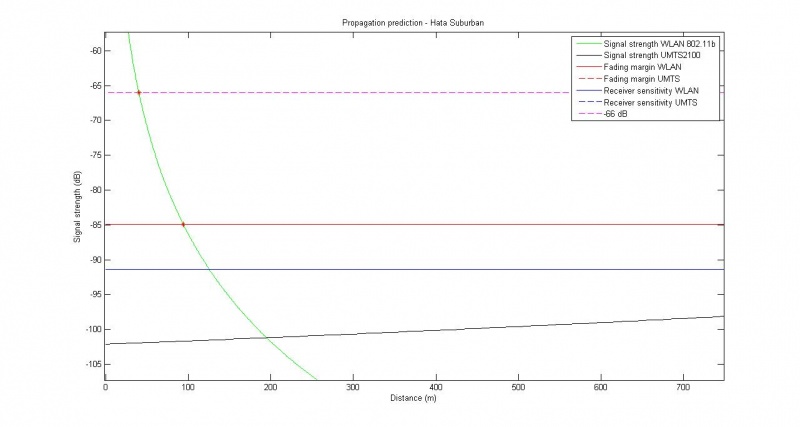
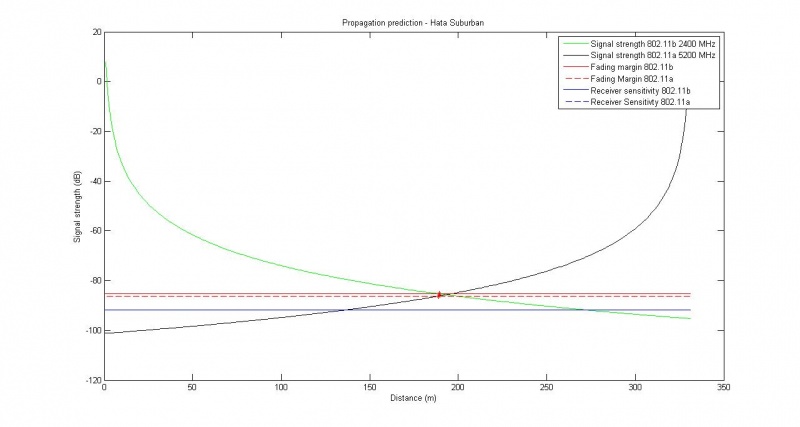
Alternate results
Assuming new value for transmitter height of UMTS (recommended numbers are 30-200m), and assuming that the Hata model does not give entirely wrong results non-recommended parameters are used, we can try to create a better estimate. Using a near 0 value for the 802.11b height (sea level lower than ground level, antenna barely above ground) and the Hata suburban model, we get these results:
- Fading margin for 802.11b hit at 94.2 m, at signal strength -84.9174.
- UMTS never dips below fading margin.
- Driving speed 20 km/h, walking speed 3 km/h.
- This gives us around 16.96 seconds from when we start driving to we hit the fading margin for 802.11b. For walking, 113.04 seconds.
- We hit -66 dB at 40.3628m. This gives us a time of 7.27 seconds from when we start to drive, or 48.44 seconds if we walk.
- If we want to start handover at -66 dB, these are the times we would use. If we want to finish handover at -66 dB, we must subtract the handover time.
Alternate code: Scenario_2_alternate_code
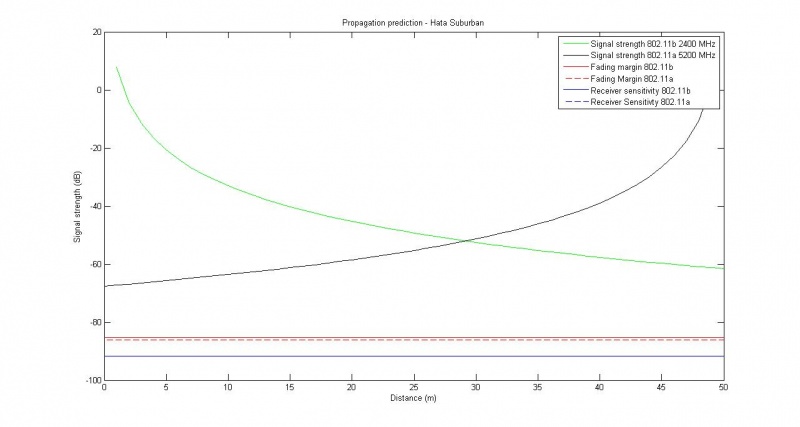
Scenario 3
Handover between 802.11a and 802.11b.
Used parameters
- Using parameters provided by scenario group:
- Suburban area
- Frequencies:
- 802.11a: 5200 MHz
- 802.11b: 2400 MHz
- Range between towers: 50 m
- Height of transmitters: 4 m
- Height of receiver: 1.8 m
- Data rate: 12.2 kbps
- Temperature: 293.15 K
- Traveling at 3 km/h
- Collected other data from Media:201211UNIK4700-BlockSeminar.pdf, page 9
Results
Assuming data rate of 11 Mb/s. Ignoring the freespace model this time and going straight for the modified Hata, we get the following graph:
We never hit the fading margin, and should have no problems doing handovers.
Code for this scenario: Scenario_3_code
Maximum distance
Objective: find maximum distance between APs at 10 Mbit/s data rate for 100 ms handover and 2 second handover. Assume walking speed of 3 km/h.
- Calculating the stretch traveled at 3 km/h in 2 seconds, we get 1.66...m. For 100 ms, we get 0.0833...m.
- The max range with these variables gives us (from base to fading margin) ~190 m for 802.11b and ~140 m for 802.11a.
- We need these to overlap for at least 1.66...m for the two second handover and at least 0.0833...m for the 100 ms handover.
- We can simply add them together and subtract the handover stretch to find the maximum distance.
- This gives us a maximum range of ~330 m for both the 2 second handover and the 100 ms handover.
Scenario 4
Handover between UMTS and UMTS, assuming same height of the transmitter towers, and that receiver height is consistent. Objective is to find the maximum distance between transmitters for various handover times and various traveling speeds.
To do this, we need the distance traveled during handover. See the table below.
| Speed | 2 sec handover | 100 ms handover |
|---|---|---|
| 120 km/h | 66.66... m | 3.33... m |
| 60 km/h | 33.33... m | 1.66... m |
| 3 km/h | 1.66... m | 0.0833... m |
Used parameters
- Using same parameters as Scenario 1, except the distance (variable).
- Removed the GSM values and plots.
Results
I could only find the distance between the transmitters rounded up/down to the nearest ten meters. Trying for the nearest whole meter, my laptop ran out of memory.
See table below for results:
| Max distance between transmitters [km] | Available handover stretch [m] |
|---|---|
| 19.96 | 67.8905 |
| 19.99 | 37.8905 |
| 20 | 27.8905 |
| 20.02 | 7.8905 |
| 20.03 | -2.1095 |
Comparing the two tables, we get:
| Speed | 2 sec handover | 100 ms handover |
|---|---|---|
| 120 km/h | ~19.96 km | ~20.02-20.03 km |
| 60 km/h | ~19.99-20 km | ~20.02-20.03 km |
| 3 km/h | ~20.02-20.03 km | ~20.02-20.03 km |
As we can see, with a 2 second handover the maximum distance varies with up to ~70 meters, and with a 100 ms one it only varies with a few meters (less than ten, probably less than five).
This can lead us to conclude that the maximum distance between transmitters is simply dependant on that their signals overlap (above fading margin) for at least the handover stretch seen in the input table.
Code can be viewed at this page: Scenario_4_code
Conclusions
Able to simulate scenario 1 reasonably well, but scenario 2 and 3 are rather inaccurate due to the short ranges in play. Scenario 4 has rather high range, though it is transmitting at maximum legal power.
see also: Media:UNIK4700-L14H12.pdf, the lecture notes from the discussion of the results, and open topics for H2013
Matlab code
- Matlab Tutorial: http://www.mathworks.se/help/matlab/index.html
- Matlab Code: http://www.mathworks.se/matlabcentral/fileexchange
- Simulation software (.m.zip): File:MATLAB.zip
- Scenario 1 code: Scenario_1_code
- Scenario 2 code (not used): Scenario_2_code
- Scenario 2 alternate code (used): Scenario_2_alternate_code
- Scenario 3 code: Scenario_3_code
- Scenario 4 code: Scenario_4_code
Programming Background
- Seminar Outline: Media:Seminar_Outline.pdf
- Radiation Pattern:Media:RadiationPattern.pdf
- Cells: Media:Cells.pdf
- Mobility: Media:Mobility.pdf
Alternative
- NS2 simulation on models provides by NIST (National Institute of Standards)
Seminar notes
- Media:201211UNIK4700-BlockSeminar.pdf handouts day 1
- Media:UNIK4700-L10H12.pdf - handouts day 2
- Video: mms://lux.unik.no/UNIK4700-JN/UNIK-20121109.wmv
References
References were provided in each section.
- ↑ Louay M.A. Jalloul, and Sam P. Alex, "Coverage Analysis for IEEE 802.16e/WiMAX Systems", IEEE Trans. on Wireless Comm., 7(11), Nov 2008, pp 4627-4635
- ↑ Filipe D. Cardoso, and Luis M. Correia, " Fading Depth Evaluation in Mobile Communications - from GSM to Future Mobile Broadband Systems", PIMRC'2002, available at DOI 10.1.1.11.4072
- ↑ COST 231, Digital mobile radio towards future generation systems, Final Report, COST Telecom Secretariat, European Commission, Brussels, Belgium, 1999, http://info.grow.inov.pt/cost231/final_report.htm