Wiki for ITS

Building .... Networks
History, Now and Future
History
Pioneers: Maxwell, Hertz,...
1G, 2G,... 5G networks
Frequencies and Standards
Future Challenges
A-Basics of Communication
Electromagnetic Signals
Radio Communication Principles
Digital communication: Signal/Noise Ratio
Signal strength and Capacity: Shannon
B-Antennas and Propagation
Free Space Propagation
Antennas, Gain, Radiation Pattern
Multipath Propagation, Reflection, Diffraction
Attenuation, Scattering
Interference and Fading (Rayleigh, Rician, …)
Mobile Communication dependencies
C-Propagation models
Environments (indoor, outdoor to indoor, vehicular)
Outdoor (Lee, Okumura, Hata, COST231 models)
Indoor (One-slope, multiwall, linear attenuation)
D-System Comparison
Proximity: RFID, NFC
Short Range: ZigBee, Bluetooth, ANT+,...
WLAN/Wifi/802.11...
Mobile: GSM, UMTS, IMT-A (WiMAX, LTE)
E-Mobility
Mobile Network mobility
IP mobility
F-Network Building
5G and Future Networks
5G Heterogeneous Networks
Basic Internet
Video Distribution Networks
Coverage simulations
Coverage simulations
Traffic simulations
Network Capacity simulations
Building .... Networks

⌘ Maxwell's Equation in a source free environment

Source free environment and free space:

$\nabla \cdot \vec E = 0 \qquad \qquad \qquad \ \ (1)$

$\nabla \times \vec E = -\frac{\partial}{\partial t} \vec B \qquad \qquad (2)$

$\nabla \cdot \vec B = 0 \qquad \qquad \qquad \ \ (3)$

$\nabla \times \vec B = \mu_0 \epsilon_0 \frac{\partial}{\partial t} \vec E \qquad \ \ \ (4)$

where div is a scalar function
$\mbox{div}\,\vec v = {\partial v_x \over \partial x} + {\partial v_y \over \partial y} + {\partial v_z \over \partial z} = \nabla \cdot \vec v$
and curl is a vector function
$\mbox{curl}\;\vec v = \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) \mathbf{i} + \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \mathbf{j} + \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \mathbf{k} = \nabla \times \vec v$

[Source: Wikipedia]

⌘ Wave equation

Taking the curl of Maxwell's equation

$\nabla \times \nabla \times \vec E = -\frac{\partial } {\partial t} \nabla \times \vec B = -\mu_0 \varepsilon_0 \frac{\partial^2 \vec E } {\partial t^2}$

$\nabla \times \nabla \times \vec B = \mu_0 \varepsilon_0 \frac{\partial } {\partial t} \nabla \times \vec E = -\mu_o \varepsilon_o \frac{\partial^2 \vec B}{\partial t^2}$

yields the wave equation:
${\partial^2 \vec E \over \partial t^2} \ - \ {c_0}^2 \cdot \nabla^2 \vec E \ \ = \ \ 0$

${\partial^2 \vec B \over \partial t^2} \ - \ {c_0}^2 \cdot \nabla^2 \vec B \ \ = \ \ 0$

with $c_0 = { 1 \over \sqrt{ \mu_0 \varepsilon_0 } } = 2.99792458 \times 10^8$ m/s

[Source: Wikipedia]

⌘ Homogeneous electromagnetic wave

A single frequency electro (E)-magnetic (B) wave is described by

$\vec E(\vec r) = E_0 e^{j(\omega t - \vec k \cdot \vec r) }$ ,

$\vec B(\vec r) = B_0 e^{j(\omega t - \vec k \cdot \vec r) }$ ,

[Source: Wikipedia]

where

$\vec r = (x, y, z)$ and $\vec k = (k_x, k_y, k_z)$ so?
$j \,$ is the imaginary unit
$\omega = 2 \pi f \,$ is the angular frequency, [rad/s]
$f \,$ is the frequency [1/s]
$e^{j \omega t} = \cos(\omega t) + j \sin(\omega t)$ is Euler's formula

with the group velocity (free space = speed of light) $c = { c_0 \over n } = { 1 \over \sqrt{ \mu \varepsilon } }$ and
the refraction index $n = \sqrt{ \mu \varepsilon \over \mu_0 \varepsilon_0$

⌘ Tasks

Calculation of a plane wave, prove that Z_0 = ... = E_x/H_y

What is the difference between a static and a dynamic field

Develop the relations for a plain wave

Assume a plane wave: $E_x, H_y$ . Show that $\frac{E_x}{H_y}=Z_0 = \sqrt{\mu_0/\varepsilon_0}$

Comments

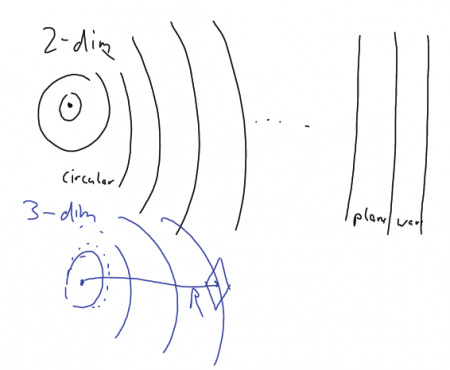
The differences between a plane wave, a cylindrical wave and a spherical wave is defined through the surface of wave. Assume propagation in z-direction

a wave having no variation in x,y direction is called a plane wave, and is represented as e.g. $\vec E(\vec r) = E_x e^{j(\omega t - k_z \cdot z) }$ ,
a wave looking like a "cylinder" is called a cylindrical wave. Such a wave is typically generated by a line source, or the diffraction at the edge of a roof
a wave looking like a "ball" is called a spherical wave. Such a wave is typically generated by a point source, e.g. a short antenna. If you move long away from the wave, then the spherical wave will become a plane wave. We talk about the far-field of an antenna, when the wave is treated like a plane wave. This is typically expressed as a phase variation being less than 90 degrees: $\varphi < 90\deg$

Comments and further reading

Q: More about wave equation in physics

A: See the good examples at http://www.physicsclassroom.com/class/waves/Lesson-2/The-Wave-Equation

Q: I still don't understand the propagation equation

A: The propagation equation describes how a wave propagates. It addresses the change from an electrical field indicating a magnetic field and vice versa. See the video from Bucknell University: https://www.youtube.com/watch?v=xkG86pwaOH0

⌘ Free space propagation

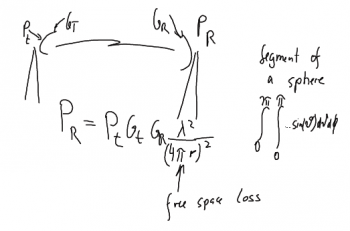
Power received in an area in a distance R from transmitter:

area of a sphere is $A_s = 4*\pi*R^2$
power transmitted from isotropic antenna is $P_t$
antenna area of receiver is $A_r = \lamda^2/4\pi$
power received in A_r = P_r

$P_r = P_t * A_r / A_s = P_r = P_t * A_r / (4*\pi*R^2)$

thus

$P_r = P_t \ G_t\ G_r\ \left (\frac{\lambda}{4\pi r} \right )^2\cdot$

convert into dB
provide examples for f = 10 MHz, 1 GHz, 100 GHz
discuss influences on radiation pattern

⌘ Tasks

Develop the propagation equation, see (http://www.antenna-theory.com/basics/friis.php)

How much is 0 dB_m and 10 dB_m?

Convert dBm to mW is: mW = 10^(x/10), x = number of dBm
Convert mW to dBm is: dBm = 10*log10(y), y = number of mW

So you get:

0 dBm = 10^(0/10) = 1 mW
10 dBm = 10^(10/10) = 10 mW

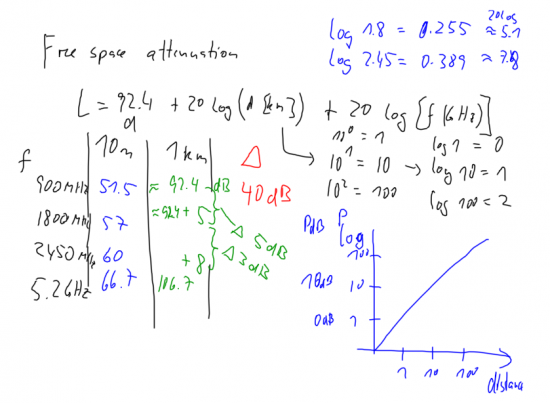
Free space attenuation $L = 92,4 + 20 \log(d \mathrm{[km]}) + 20 \log(f \mathrm{[/GHz]})$

Comments

Free space propagation from a transmit (t) to a receive (r) station.

Calculation of free space attenuation. Note the increased free-space attenuation of approx 5 dB from 900 to 1800 MHz, and a further increase of 3 dB from 1800 (GSM 1800) to 2450 MHz (802.11b). Note also that increasing the distance by a factor of 10 will increase the power requirements by 20 dB.

Have in mind that normal communication is always worse than the "ideal" free space communication. You have shadowing, reflections, interference, and other influences increasing the path loss. An example is the Bluetooth communication between your mobile phone and your headset, where your body absorbs energy and shadows for direct communication.

Free space propagation Calculation: http://spreadsheets.google.com/pub?key=p0EyjWrbirGKJXK43uluJfg

B1-Free Space Propagation

Contents

⌘ Maxwell's Equation in a source free environment

⌘ Wave equation

⌘ Homogeneous electromagnetic wave

⌘ Tasks

Comments

Comments and further reading

⌘ Free space propagation

⌘ Tasks

Comments

Navigation menu

Personal tools

Namespaces

Variants

Views

Actions

Search

Main

Applied Research for

List of

Forms (create or edit)

Help

Tools