Difference between revisions of "A4-Signal Strength and Capacity"
From its-wiki.no
Josef.Noll (Talk | contribs) |
Josef.Noll (Talk | contribs) |
||
| Line 10: | Line 10: | ||
More detailed discussions on these effects can be found in the literature indicated above. | More detailed discussions on these effects can be found in the literature indicated above. | ||
| + | |||
| + | |||
| + | =⌘ Signal/noise ratio = | ||
| + | <math> \mathrm{SNR} = {P_\mathrm{signal} \over P_\mathrm{noise}} </math> | ||
| + | |||
| + | <math> \mathrm{SNR (dB)} = 10 \log_{10} \left ( {P_\mathrm{signal} \over P_\mathrm{noise}} \right ) </math>, | ||
| + | |||
| + | where ''P'' is average power | ||
| + | |||
| + | * <span style="color:#000B80"> why talking about noise? | ||
| + | * <span style="color:#000B80"> dB, <math>\mbox{dB}_m,\ \mbox{dB}_a </math> | ||
| + | * <span style="color:#000B80"> near-far problem | ||
| + | [source: Wikipedia] | ||
| + | |||
| + | =⌘ Shannon Theorem = | ||
| + | * The fundamental theorem of information theory, or just Shannon's theorem, was first presented by Claude Shannon in 1948. | ||
| + | * Given a noisy channel with channel capacity ''C'' and information transmitted at a rate ''R'', then if ''R < C'' there exist codes that allow the probability of error at the receiver to be made arbitrarily small. This means that theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, ''C''. | ||
| + | |||
| + | * See [[File:LarsLundheim-Telektronikk2002.pdf]]: The channel capacity of a band-limited information transmission channel with additive white, Gaussian noise. This capacity is given by an expression often known as “Shannon’s formula”: <math> C = W\ \mathrm{log}_2(1+P/N) </math> [bits/s] | ||
| + | |||
| + | with ''W'' as system bandwidth, and <math> P/N = \frac{P}{N_0 W} </math> in case of interference free environment, otherwise <math> N_0 W + N_\mathrm{interference} </math>, where <math>N_0 = k_B T_K</math> with <math>k_B</math> as Boltzmann constant and <math>T_K</math> as temperature in Kelvin. | ||
| + | |||
| + | Exercises: | ||
| + | * If the SNR is 20 dB, and the bandwidth available is 4 kHz, what is the capacity of the channel? | ||
| + | * If it is required to transmit at 50 kbit/s, and a bandwidth of 1 MHz is used, what is the minimum S/N required for the transmission? | ||
| + | |||
| + | [source: Wikipedia, Telektronikk 2002] | ||
| + | |||
| + | == Comments== | ||
| + | [[File:F3-2.png|450px|right|Shannon theorem and application to radio propagation]] | ||
Revision as of 22:28, 20 September 2014
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
Main focus in the previous lectures was on propagation effects. We will first repeat the main conclusions from last lecture on electromagnetic signals, and then introduce the capacity of a system based on Shannon's theorem.
New literature:
- J. Noll, K. Baltzersen, A. Meiling, F. Paint , K. Passoja, B. H. Pedersen, M. Pettersen, S. Svaet, F. Aanvik, G. O. Lauritzen. '3rd generation access network considerations'. selected pages from Unik/FoU R 3/99, Jan 1999 (.pdf]])
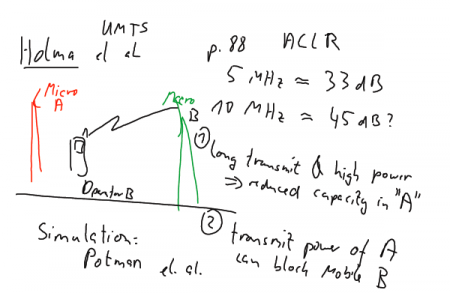
- H. Holma, A. Toskala (eds.), "WCDMA for UMTS", John Wiley & sons, Oct 2000, selected pages
Comments
Figure: Illustrating reduction of capacity in network A (top) and blinding of phones in cell (B)
More detailed discussions on these effects can be found in the literature indicated above.
⌘ Signal/noise ratio
,
where P is average power
- why talking about noise?
- dB,
- near-far problem
[source: Wikipedia]
⌘ Shannon Theorem
- The fundamental theorem of information theory, or just Shannon's theorem, was first presented by Claude Shannon in 1948.
- Given a noisy channel with channel capacity C and information transmitted at a rate R, then if R < C there exist codes that allow the probability of error at the receiver to be made arbitrarily small. This means that theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, C.
- See File:LarsLundheim-Telektronikk2002.pdf: The channel capacity of a band-limited information transmission channel with additive white, Gaussian noise. This capacity is given by an expression often known as “Shannon’s formula”:
[bits/s]
with W as system bandwidth, and in case of interference free environment, otherwise
, where
with
as Boltzmann constant and
as temperature in Kelvin.
Exercises:
- If the SNR is 20 dB, and the bandwidth available is 4 kHz, what is the capacity of the channel?
- If it is required to transmit at 50 kbit/s, and a bandwidth of 1 MHz is used, what is the minimum S/N required for the transmission?
[source: Wikipedia, Telektronikk 2002]
Comments