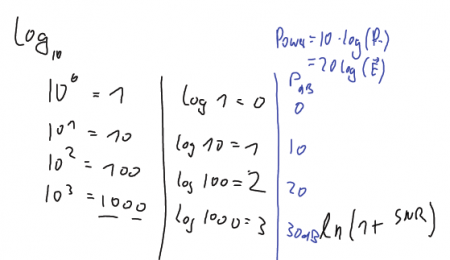Difference between revisions of "A4-Signal Strength and Capacity"
Josef.Noll (Talk | contribs) |
Josef.Noll (Talk | contribs) (→Range simulations) |
||
| Line 74: | Line 74: | ||
|} | |} | ||
=== Range simulations === | === Range simulations === | ||
| − | <! | + | <!------- taken from UNIK4700 interference ----> |
'''2009: Matlab simulation results from Thomas, Espen og Øystein. [[File:RangeSimulation.zip]]''' | '''2009: Matlab simulation results from Thomas, Espen og Øystein. [[File:RangeSimulation.zip]]''' | ||
| Line 83: | Line 83: | ||
* <span style="color:#000B80"> minimum GSM receiver sensitivity | * <span style="color:#000B80"> minimum GSM receiver sensitivity | ||
* ''other questions related to radio''? | * ''other questions related to radio''? | ||
| − | |||
== Comments== | == Comments== | ||
Revision as of 09:33, 21 September 2014
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
Main focus in the previous lectures was on propagation effects. We will first repeat the main conclusions from last lecture on electromagnetic signals, and then introduce the capacity of a system based on Shannon's theorem.
New literature:
- J. Noll, K. Baltzersen, A. Meiling, F. Paint , K. Passoja, B. H. Pedersen, M. Pettersen, S. Svaet, F. Aanvik, G. O. Lauritzen. '3rd generation access network considerations'. selected pages from Unik/FoU R 3/99, Jan 1999 (.pdf]])
- H. Holma, A. Toskala (eds.), "WCDMA for UMTS", John Wiley & sons, Oct 2000, selected pages
Contents
Comments
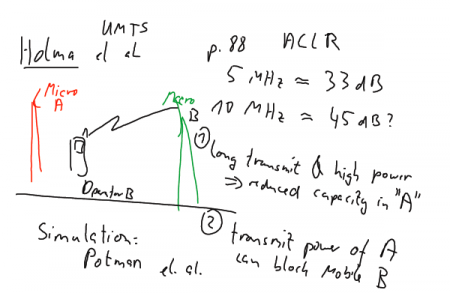
Figure: Illustrating reduction of capacity in network A (top) and blinding of phones in cell (B)
More detailed discussions on these effects can be found in the literature indicated above.
⌘ Signal/noise ratio
,
where P is average power
- why talking about noise?
- dB,
- near-far problem
[source: Wikipedia]
⌘ Shannon Theorem
- The fundamental theorem of information theory, or just Shannon's theorem, was first presented by Claude Shannon in 1948.
- Given a noisy channel with channel capacity C and information transmitted at a rate R, then if R < C there exist codes that allow the probability of error at the receiver to be made arbitrarily small. This means that theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, C.
- See File:LarsLundheim-Telektronikk2002.pdf: The channel capacity of a band-limited information transmission channel with additive white, Gaussian noise. This capacity is given by an expression often known as “Shannon’s formula”:
[bits/s]
with W as system bandwidth, and in case of interference free environment, otherwise
, where
with
as Boltzmann constant and
as temperature in Kelvin.
Exercises:
- If the SNR is 20 dB, and the bandwidth available is 4 kHz, what is the capacity of the channel?
- If it is required to transmit at 50 kbit/s, and a bandwidth of 1 MHz is used, what is the minimum S/N required for the transmission?
[source: Wikipedia, Telektronikk 2002]
⌘ Shannon - examples
[bits/s]
Examples
- calculate capacity for W= 200 kHz, 3.8 Unik/MHz, 26 Unik/MHz, (all cases P/N = 0 dB, 10 dB, 20 dB)
Comments
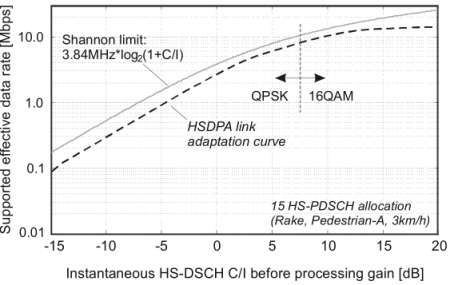
Figure: Calculation of Shannon capacity for GSM (GPRS, EDGE), UMTS (packet data, HSDPA) and 802.11b
Figure: Log_10 funtion and related power. The power expressed in dB is 10 times the log_10 of the normalised power.
There are also the abbreviations
-
stands for power with respect to 1 mW. How much is 0 dB_m and 10 dB_m?
-
Power of a sound (or music).
⌘ Cell capacity in UMTS
UMTS has good efficiency with respect to Shannon
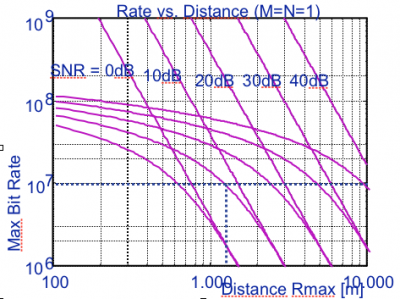
⌘ Range versus SNR
|
[Source:Valenzuela, BLAST project] |
Range simulations
2009: Matlab simulation results from Thomas, Espen og Øystein. File:RangeSimulation.zip
Let's start What have we learned?
- antenna characteristics and gain
- what happens if I double the frequency (900 - 1800 - 2400 MHz)?
- minimum GSM receiver sensitivity
- other questions related to radio?
Comments
Range
[Source Valenzuela, BLAST project]
why is there no relation to frequency?
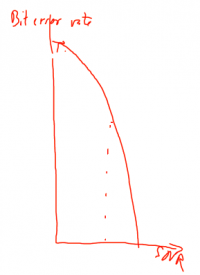
Relation of Bit Error Rate and SNR
| The Bit Error Rate (BER) describes the statistics of bits being "false" due to propagation effects. BER is typically described in BER = 10-3.
Typical values for reasonable communications are:
|