B2-Antennas
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
Contents
⌘ B2-Antennas
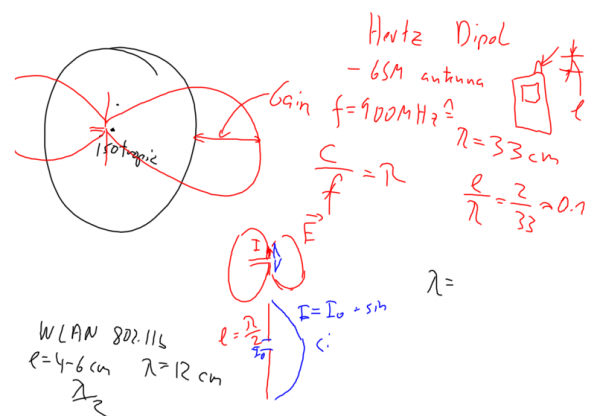
Keywords: Antennas, Hertz Dipol, Antenna Gain
⌘ B2-Antenna Basics
The gain is the radiation intensity of an antenna into the main direction as compared to an isotropic antenna (omnidirectional). For a perfect antenna without any losses, the gain G will be identical to the directivity D.
⌘ Antenna pattern
If the antenna pattern is known, then the gain can be easily calculated.
- Isotropic antenna = point source:
- Hertz Dipol = Short dipol:
-
-Dipol:
- draw electrical field of dipole
- Aperture antennas:
, with
, leads to gain of
- examples of reflector antennas (effective aperture)
For more info, see intro course: http://www.cv.nrao.edu/course/astr534/AntennaTheory.html
⌘Example:
Gain calculation for a -antenna
calculate the gain of a
antenna, given that the electrical field can be described as:
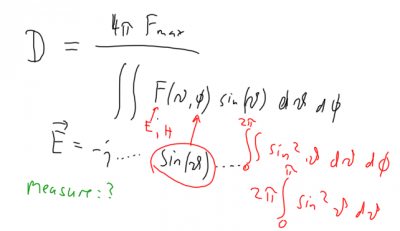
Practical measurement of antenna gain: Compare the value of the electromagnetic field in the main direction of radiation with the gain of an isotropic antenna (or the gain of a known antenna). Best interaction is for antennas with length l approx lambda/2 ... lambda. Examples are provided for stubb antennas on GSM phones and typical WLAN 802.11b antennas.
Calculate the gain of a lambda/2 antenna, given that the electrical field of the antenna is given through a sin(theta) relation
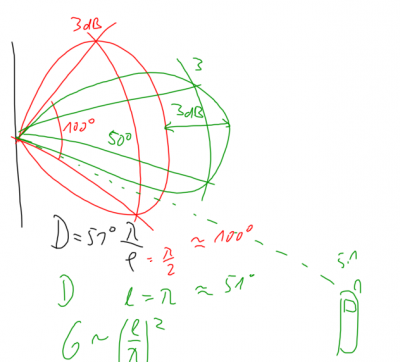
Doubling antenna gain (+3 dB) will decrease the antenna pattern by a factor of two. This might cause mobile phones to fall outside of the radiation range.
⌘Example
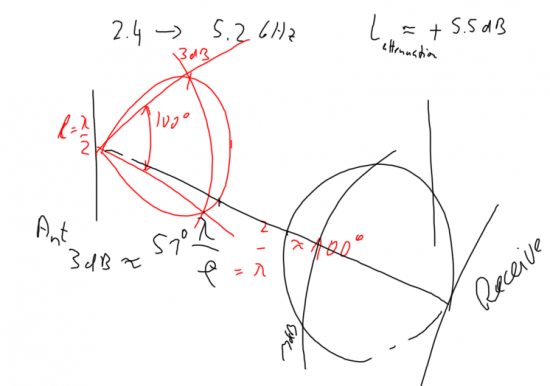
What happens if I move from 2.4 Unik/GHz (802.11b) band to 5.1 Unik/GHz (802.11a)?
- Free space propagation
- antenna gain
- total power budget
- other factors?
Increase frequency from 2.4 to 5.2 Unik/GHz will yield to an additional free-space attenuation of 5.5 dB. If the same antennas are used, then this attenuation will be overcompensated by the antenna gain of both the transmit and the receive antenna.
However, the antenna characteristic will change significantly when doubling the frequency. Assuming that no mismatch occurs at the antenna feed, the width of the antenna beam will be reduced by a factor of two (relation lambda/l). This means that if receive and transmit antennas don't point towards each other, significant antenna gain loss might be seen.
Antenna interaction
- from antenna design, what have we learned?
- which length/area is best (as compared to
to interact with an electromagnetic wave)?
⌘ Further Reading
- Media:Antennas_for_communications_Haavard.pdf (by Håvard Austad)
- Book: Stallings; Wireless Communications & networks
- Book:Thorvaldsen & Henne; Planning of line-of-sight radio relay system
- Book:Balanis: Antenna Therory: Analysis and Design