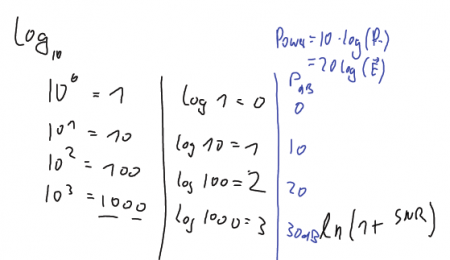Radio propagation equation (A4,B1)
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
Radio propagation equation (A4,B1)
| Course | UNIK4700, UNIK9700 |
|---|---|
| Title | Radio propagation for mobile and wireless communications |
| Lecture date | 2017/09/12 1315-1600h |
| presented | by Josef Noll |
| Objective | The objective of this lecture is to explain the principles of radio propagation. |
| Learning outcomes | What will we learn today
|
| Pensum (read before) | |
| References (further info) | References: |
| Keywords | Propagation, Free space attenuation, propagation equation, transmit power, Attenuation, Permittivity, Permeability, EIRP, Reflection, Diffraction, Scattering, Shannon |
this page was created by Special:FormEdit/Lecture, and can be edited by Special:FormEdit/Lecture/Radio propagation equation (A4,B1).
Forelesning fra Scheme@ifi.uio.no - IP: 10.64.127.141,
Test yourself, answer these questions
- Convert to dB, dBm:
- What is the exact difference between permeability and permittivity?
- What is Relative permittivity? and Relative Permeability?
- Define Propagation constant
left over from 5Sep2017
- ) Video recording is now in place, please check on the UNIK4700 for the format of the .wmv recordings, or select from https://plus.google.com/communities/107897964181233758835
- ) Regarding the assignments: Please check 19Sep and 26Sep for the topics to be presented
Lecture notes
- Lecture Notes 2017: Media:20170912_UNIK4700h17handouts.pdf, Video recording: mms://lux.unik.no/UNIK4700-JN/UNIK-20170912.wmv (still to come)
- Media:UNIK4700-L1-Overview.pdf - topics and overview
- Media:UNIK4700h15-RadioPropagation.pdf
- Media:UNIK4700h14-RadioPropagation.pdf
- Video: mms://lux.unik.no/UNIK4700-JN/UNIK-20140912.wmv
- Streaming
- Media:UNIK4700-L3H13.pdf
- Media:UNIK4700-L4H12.pdf
focus 2016
- Structured presentation of the topics of the course, see Media:UNIK4700-L1-Overview.pdf
- Application case, e.g. Tanzania, Country in Africa
- Assignments and work for 2nd presentation
Focus 2015
- Presentation of Slobodan on "Propagation equation"
- Presentation of Marshed on "Radio channels in WPAN"
- also: Shannon, Capacity
- define 2nd presentation
- Title
- UNIK4700/UNIK9700 Signal and Capacity
- Author
- Josef Noll,
- Footer
- Radio propagation equation (A4,B1)
- Subfooter
- UNIK4700/UNIK9700
⌘ UNIK 4700: Radio & Mobility
3rd lecture block
- Free space propagation equation, what is the power level at a receive antenna, see Media:PropagationConstant.pdf for a more detailed explanation of the terms being used here
- Capacity of mobile and wireless propagation,
⌘ Signal Strength and Capacity
⌘ A4-Signal Strength and Capacity
Main focus in the previous lectures was on propagation effects. We will first repeat the main conclusions from last lecture on electromagnetic signals, and then introduce the capacity of a system based on Shannon's theorem.
New literature:
- J. Noll, K. Baltzersen, A. Meiling, F. Paint , K. Passoja, B. H. Pedersen, M. Pettersen, S. Svaet, F. Aanvik, G. O. Lauritzen. '3rd generation access network considerations'. selected pages from FoU R 3/99, Jan 1999
- H. Holma, A. Toskala (eds.), "WCDMA for UMTS", John Wiley & sons, Oct 2000, selected pages
Comments
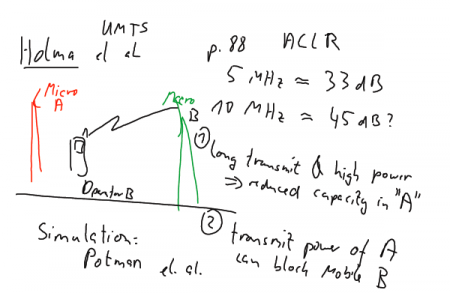
Figure: Illustrating reduction of capacity in network A (top) and blinding of phones in cell (B)
More detailed discussions on these effects can be found in the literature indicated above.
⌘ Signal/noise ratio
,
where P is average power
- why talking about noise?
- dB,
- near-far problem
[source: Wikipedia]
⌘ Shannon Theorem
- The fundamental theorem of information theory, or just Shannon's theorem, was first presented by Claude Shannon in 1948.
- Given a noisy channel with channel capacity C and information transmitted at a rate R, then if R < C there exist codes that allow the probability of error at the receiver to be made arbitrarily small. This means that theoretically, it is possible to transmit information nearly without error at any rate below a limiting rate, C.
- See File:LarsLundheim-Telektronikk2002.pdf: The channel capacity of a band-limited information transmission channel with additive white, Gaussian noise. This capacity is given by an expression often known as “Shannon’s formula”:
[bits/s]
with W as system bandwidth, and in case of interference free environment, otherwise
, where
with
as Boltzmann constant and
as temperature in Kelvin.
⌘ Shannon - formula
[bits/s]
Exercises
- calculate capacity for W= 200 kHz, 3.8 MHz, 26 MHz, (all cases P/N = 0 dB, 10 dB, 20 dB)
- If the SNR is 20 dB, and the bandwidth available is 4 kHz, what is the capacity of the channel?
- If it is required to transmit at 50 kbit/s, and a bandwidth of 1 MHz is used, what is the minimum S/N required for the transmission?
[source: Wikipedia, Telektronikk 2002]
Comments
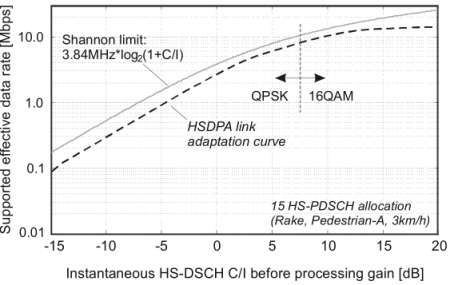
Figure: Calculation of Shannon capacity for GSM (GPRS, EDGE), UMTS (packet data, HSDPA) and 802.11b
Figure: Log_10 function and related power. The power expressed in dB is 10 times the log_10 of the normalised power.
There are also the abbreviations
-
stands for power with respect to 1 mW. How much is 0 dB_m and 10 dB_m?
-
Power of a sound (or music).
⌘ Cell capacity in UMTS
UMTS has already good spectrum efficiency with respect to Shannon.
- Modulation schemes like QPSK and 16-QAM are applied to achieve higher bandwidth.
- Higher modulation schemes need a higher signal to noise ration, Why?
⌘Multiple-Input, Multiple-Output: MIMO
Using multiple paths (wave propagation) in a MIMO system to enhance the bandwidth of the system.
Comments
The dominating factor in capacity is the bandwidth. If you double the bandwidth being used at a given frequency, you double the capacity. However, bandwidth is limited, both due to spectrum licensing and due to electronics. Typical electronic amplifiers have a linearity of 10%, meaning: An amplifier operating at 1.8 GHz will have 180 MHz bandwidth. If you want to achieve more bandwidth, you need to invest in more expensive receivers and transmitters, pushing the costs for the hardware.
Wifi at 2.4 GHz is a typical example using cheap hardware. The ISM band ranges from 2400 to 2485 MHz, and a receiver or transmitter needs only to linearity of 85/2400 = 3.5%
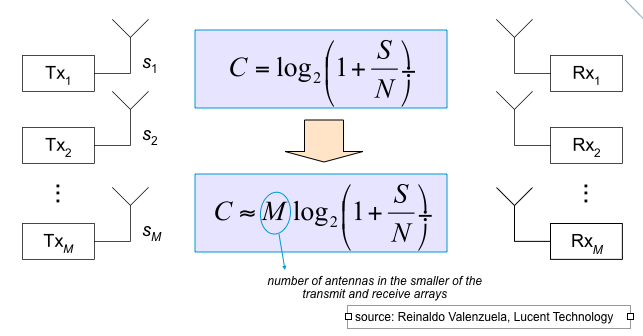
The MIMO principle allows that every antenna on the transmit side can communicate to all other antennas on the receiver side. Example: a 3 x 2 MIMO system will have 3 transmit () and 2 receive (
) antenna. In that case,
will have waves travelling to both
and
. The more these channels T_1 -> R_1 and T_1 -> R_2 are independent, the more information can be transferred.
The effect on capacity is given by the number of spatial streams, being the minimum of the number of antennas on transmit and receive side. In our case of a 3 x 2 MIMO systems we will have an increase of .
For further readings, I recomment: http://mwrf.com/markets/understanding-benefits-mimo-technology
⌘MIMO laptop
Figure: A MIMO equipped laptop (Source:Valenzuela, BLAST project)
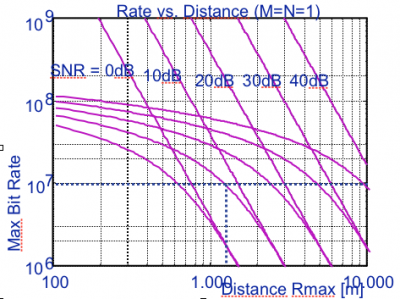
⌘ Range versus SNR
|
[Source:Valenzuela, BLAST project] |
Lessions learned
Let's start What have we learned?
- antenna characteristics and gain
- what happens if I double the frequency (900 - 1800 - 2400 MHz)?
- minimum GSM receiver sensitivity
- other questions related to radio?
Comments
Range
[Source Valenzuela, BLAST project]
why is there no relation to frequency?
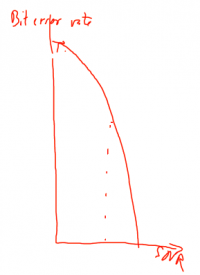
Relation of Bit Error Rate and SNR
⌘ Free Space Propagation
⌘ Maxwell's Equation in a source free environment
Source free environment and free space:
where div is a scalar function
and curl is a vector function
[Source: Wikipedia]
⌘ Wave equation
Taking the curl of Maxwell's equation
yields the wave equation:
with m/s
[Source: Wikipedia]
⌘ Homogeneous electromagnetic wave
A single frequency electro (E)-magnetic (B) wave is described by
,
,
[Source: Wikipedia]
where
-
and
so?
-
is the imaginary unit
-
is the angular frequency, [rad/s]
-
is the frequency [1/s]
-
is Euler's formula
with the group velocity (free space = speed of light) and
the refraction index
⌘ Tasks
- What is the difference between a static and a dynamic field
- Develop the relations for a plain wave
- Assume a plane wave:
. Show that
Comments
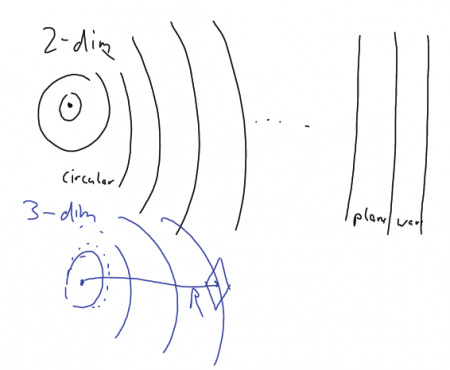
The differences between a plane wave, a cylindrical wave and a spherical wave is defined through the surface of wave. Assume propagation in z-direction
- a wave having no variation in x,y direction is called a plane wave, and is represented as e.g.
,
- a wave looking like a "cylinder" is called a cylindrical wave. Such a wave is typically generated by a line source, or the diffraction at the edge of a roof
- a wave looking like a "ball" is called a spherical wave. Such a wave is typically generated by a point source, e.g. a short antenna. If you move long away from the wave, then the spherical wave will become a plane wave. We talk about the far-field of an antenna, when the wave is treated like a plane wave. This is typically expressed as a phase variation being less than 90 degrees:
Comments and further reading
Q: More about wave equation in physics
- A: See the good examples at http://www.physicsclassroom.com/class/waves/Lesson-2/The-Wave-Equation
Q: I still don't understand the propagation equation
- A: The propagation equation describes how a wave propagates. It addresses the change from an electrical field indicating a magnetic field and vice versa. See the video from Bucknell University: https://www.youtube.com/watch?v=xkG86pwaOH0
⌘ Free space propagation
Power received in an area in a distance R from transmitter:
- area of a sphere is
- power transmitted from isotropic antenna is
- antenna area of receiver is
- power received in A_r = P_r
thus
- convert into dB
- provide examples for f = 10 MHz, 1 GHz, 100 GHz
- discuss influences on radiation pattern
⌘ Tasks
Develop the propagation equation, see (http://www.antenna-theory.com/basics/friis.php)
How much is 0 dB_m and 10 dB_m?
- Convert dBm to mW is: mW = 10^(x/10), x = number of dBm
- Convert mW to dBm is: dBm = 10*log10(y), y = number of mW
So you get:
- 0 dBm = 10^(0/10) = 1 mW
- 10 dBm = 10^(10/10) = 10 mW
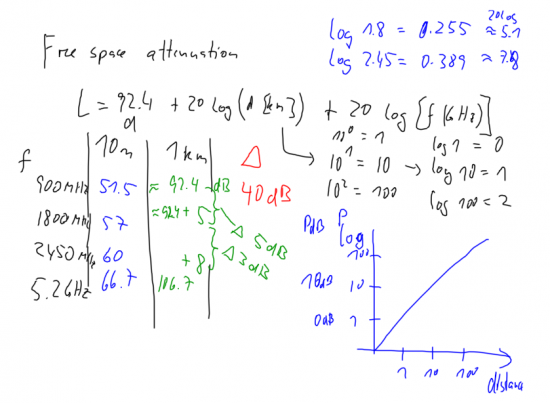
Free space attenuation
Comments
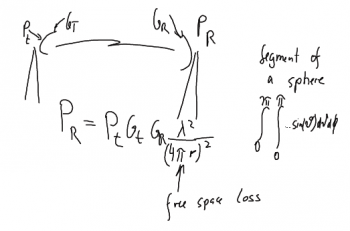
|
Free space propagation from a transmit (t) to a receive (r) station. |
Calculation of free space attenuation. Note the increased free-space attenuation of approx 5 dB from 900 to 1800 MHz, and a further increase of 3 dB from 1800 (GSM 1800) to 2450 MHz (802.11b). Note also that increasing the distance by a factor of 10 will increase the power requirements by 20 dB.
Have in mind that normal communication is always worse than the "ideal" free space communication. You have shadowing, reflections, interference, and other influences increasing the path loss. An example is the Bluetooth communication between your mobile phone and your headset, where your body absorbs energy and shadows for direct communication.
Free space propagation Calculation: http://spreadsheets.google.com/pub?key=p0EyjWrbirGKJXK43uluJfg