Antennas and their communication parameters (B2-B3)
| Wiki for ITS | ||||||
|---|---|---|---|---|---|---|
|
Antennas and their communication parameters (B2-B3)
| Course | UNIK4700, UNIK9700 |
|---|---|
| Title | Antennas and their communication parameters |
| Lecture date | 2017/10/03 1300-1600 |
| presented | by Josef Noll |
| Objective | Discussion on Antennas and their communication parameters |
| Learning outcomes | What will we learn today:
|
| Pensum (read before) | Antenna Parameters
TDMA, FDMA and CDMA in Mobile Communications
|
| References (further info) | References: |
| Keywords | antennas, beamwidth, radiation pattern, gain, directivity, input impedance |
this page was created by Special:FormEdit/Lecture, and can be edited by Special:FormEdit/Lecture/Antennas and their communication parameters (B2-B3).
Test yourself, answer these questions
- What two functions are performed by antenna?
- What is isotropic antenna?
- What factors determine antenna gain?
- What is meant by radiation pattern?
- What is polarisation ? What are its types?
- If a high frequency has a short wavelength, what wavelength does a low frequency have?
- What is fading?
- What is the difference between diffraction and fading?
- What is the difference between fast and slow fading?
- What is the difference between flat and selective fading?
Lecture notes
- Media:UNIK4700v17-Antennas.pdf
- Media:UNIK4700v16-Antennas.pdf
- Media:UNIK4700v14-Antennas.pdf
- Free Space propagation, see last slides in Radio_propagation_equation
- more information: propagation in free space, last slide in http://wiki.unik.no/index.php/Courses/UNIK4700signal
- Introduction to Antennas - http://wiki.unik.no/index.php/Courses/UNIK4700propagation
Earlier years
- Title
- UNIK4710/UNIK9710 Antennas
- Author
- Josef Noll
- Footer
- Antennas and their communication parameters (B2-B3)
- Subfooter
- UNIK4710/UNIK9710
Topic selection for next week
- 10Oct: present your ideas
- identify the parameters you will look at (prepare for sensitivity analysis and own evaluation)
- don't simply present, but rather show your understanding of a "sub-set" og the topic
- perform an evaluation towards the parameters used
⌘ B2-Antennas
Keywords: Antennas, Hertz Dipol, Antenna Gain
⌘ B2-Antenna Basics
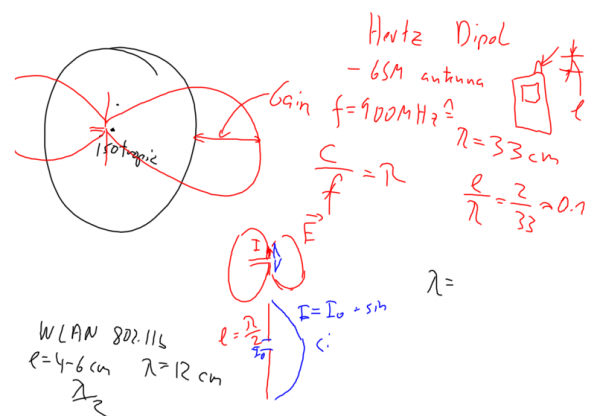
The gain is the radiation intensity of an antenna into the main direction as compared to an isotropic antenna (omnidirectional). For a perfect antenna without any losses, the gain G will be identical to the directivity D.
⌘ Antenna pattern
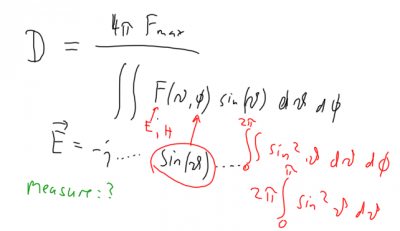
If the antenna pattern is known, then the gain can be easily calculated.
- Isotropic antenna = point source:
- Hertz Dipol = Short dipol:
-
-Dipol:
- draw electrical field of dipole
- Aperture antennas:
, with
, leads to gain of
- examples of reflector antennas (effective aperture)
For more info, see intro course: http://www.cv.nrao.edu/course/astr534/AntennaTheory.html
⌘Example:
Gain calculation for a -antenna
calculate the gain of a
antenna, given that the electrical field can be described as:
Practical measurement of antenna gain: Compare the value of the electromagnetic field in the main direction of radiation with the gain of an isotropic antenna (or the gain of a known antenna). Best interaction is for antennas with length l approx lambda/2 ... lambda. Examples are provided for stubb antennas on GSM phones and typical WLAN 802.11b antennas.
Calculate the gain of a lambda/2 antenna, given that the electrical field of the antenna is given through a sin(theta) relation
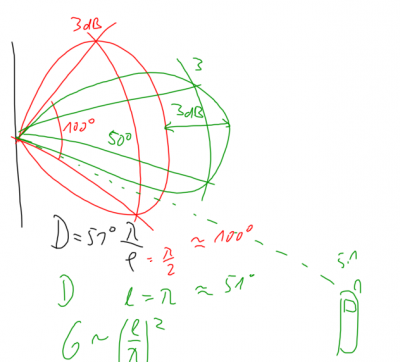
Doubling antenna gain (+3 dB) will decrease the antenna pattern by a factor of two. This might cause mobile phones to fall outside of the radiation range.
⌘Example
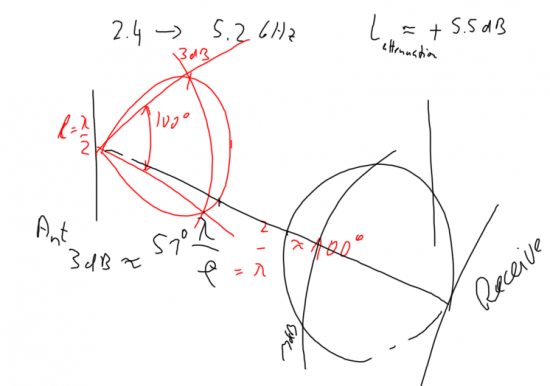
What happens if I move from 2.4 Unik/GHz (802.11b) band to 5.1 Unik/GHz (802.11a)?
- Free space propagation
- antenna gain
- total power budget
- other factors?
Increase frequency from 2.4 to 5.2 Unik/GHz will yield to an additional free-space attenuation of 5.5 dB. If the same antennas are used, then this attenuation will be overcompensated by the antenna gain of both the transmit and the receive antenna.
However, the antenna characteristic will change significantly when doubling the frequency. Assuming that no mismatch occurs at the antenna feed, the width of the antenna beam will be reduced by a factor of two (relation lambda/l). This means that if receive and transmit antennas don't point towards each other, significant antenna gain loss might be seen.
Antenna interaction
- from antenna design, what have we learned?
- which length/area is best (as compared to
to interact with an electromagnetic wave)?
⌘ Further Reading
- Media:Antennas_for_communications_Haavard.pdf (by Håvard Austad)
- Book: Stallings; Wireless Communications & networks
- Book:Thorvaldsen & Henne; Planning of line-of-sight radio relay system
- Book:Balanis: Antenna Therory: Analysis and Design
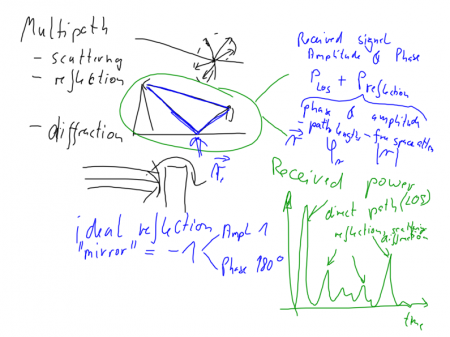
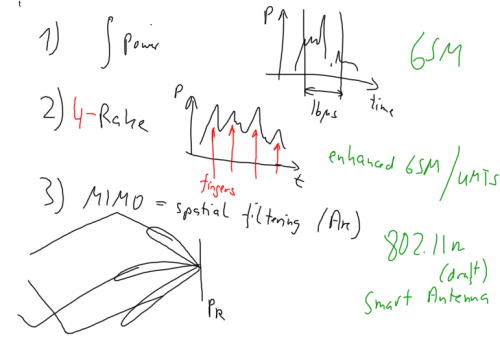
⌘ B3-Multipath Propagation
⌘Multipath and how to use it
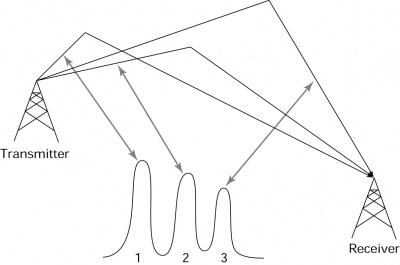
|
Multipath propagation can be used through
|
Note: The mobile phone users will typically not have a direct link between the mobile phone and the antennas of the base station in a typical environment. Such a situation, where the mobile communication has to go "around a building" or "around the corner" are called NLOS, non Line-of-Sight connection. As compared to a Line-of-Sight LOS connection the signal is typically reduced by some 20-30 dB.
⌘ Boundary conditions
- What is happening on electrical walls, magnetic walls?
Scattering, reflection and diffraction (explain differences) are the three major components in wave propagation. Ideal reflection environments are characterised through
⌘Comments
⌘ Reflection
Related physics
Free Space impedance as connection of permeability
and permittivity
.
. The unit of
is
.
The unit of is Farad/m:
Diffraction
Diffraction is the transforming of a wave at an object, typical edge of a house ("edge diffraction") or the roof-top
Scattering
Interaction with object being about the same size as the wavelength,
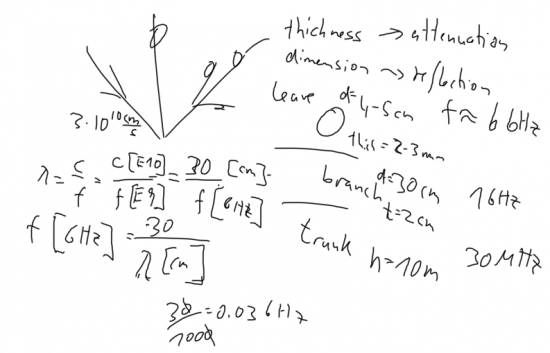
⌘ Interaction of electromagnetic waves with the Environment
Examples are:
- leaves will mainly interact around 6 Unik/GHz: thickness will attenuate, whereas reflection is due to diameter of leaves
- branches will have main interaction at about 1 Unik/GHz
- the tree trunk will interact with almost all frequencies at 30 Unik/MHz and above.
⌘ Attenuation in walls
| Attenuation in material follows typical an exponential behaviour. | 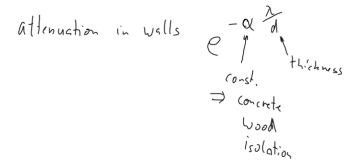
|
⌘Attenuation parameters for 2.4 GHz
| Obstacle | Attenuation |
|
|---|---|---|
| Brick wall with window | 2 | |
| Brick wall next to metal door | 3 | |
| Cinder Block wall | 4 | |
| Office wall | 6 | |
| Metal door in office wall | 6 | |
| Metall door in brick wall | 12.4 | |
| Floor | 30 |
Measurements performed for European building
(Source:Hydra Deliverable D5.4, p 12)
⌘ Path loss calculation
Hydra pass loss approximation
- relation between fading margin and receiver sensitivity